题目描述
给你一个 $ n\ast m $ 的棋盘,有一个 $ 1\ast 1\ast 2 $ 的长方体竖直放在 (1,1)上,你可以将其在棋盘上滚动,你的目标是让其竖直放在 ( n , m ) 上,问至少需要多少次操作。(放倒、竖直、翻滚)
输入
一行,两个整数n,m (n<=m)
输出
需要最少时间能从(1,1)到达(n,m),如果无解输出 $ impossible $ .
样例输入
1 1
样例输出
0
提示
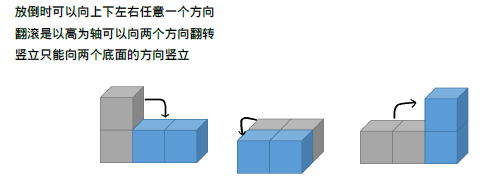
分析
这个题目我的做法其实比较暴力,因为和队友赌能不能1Y ,我甚至怂到写暴力对拍了....
闲话少说,下面看分析.
其实还是比较好想的.
首先我们考虑哪种情况是 impossible .比较好观察的是,当n和m足够大的时候就一定可达
所以我们只用找到一个n和m可达的下界就行了
然后就可以发现只有当n和m都小于3的时候会有impossible的情况(因为转不动....
接下来分析其他情况,首先比较好分析的是,如果n%3==1&&m%3==1的话,答案可以显然得到是 $(n/3+m/3)\ast 2$
剩下的同理搞搞就行了,大体情况见下表.

比较显然的是,加的那一项和n,m%3为2的数量一致,然后就是代码啦...
代码
给大佬递上我奇丑无比的代码 (/ω\)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
using namespace std;
int main(){
int n,m;
while(scanf("%d%d",&n,&m)!=EOF){
if(n<=2){
if(m%3==1) cout<<m/3*2+n-1<<endl;
else cout<<"impossible"<<endl;
}else if(n==3&&m==3) cout<<8<<endl;
else if(n==3){
if(m%3==0) cout<<m/3*2+4<<endl;
else if(m%3==1) cout<<(m+2)/3*2<<endl;
else cout<<m/3*2+5<<endl;
}else {
int ans = (n/3+m/3)*2;
ans+=(m%3==2)+(n%3==2);
cout<<ans<<endl;
}
}
return 0;
}

