作者自己辛苦原创,如有错误or转载or其他用途请联系qq:669415029,谢谢
1.利用反证法容易得到,如果$n$和$m$都是奇数,那么$n*m$也是奇数,显然不可覆盖,所以$n$和$m$至少有一个偶数
2.我们定义行号从上到下为$1\dots m$,列号从左到右为$1\dots n$,然后我们就可以得到被切掉的那个方块只可能是奇数行奇数列,或者偶数行偶数列,我们考虑对这两种方案分别进行构造来得到我们想要的答案.
- 奇数行奇数列:对于和他在同一行同一列的方块来说,因为他去掉了,所以剩下的一定是可以匹配的偶数,也就是说我们可以匹配上这一行一列,对于剩下的一定都是偶数行偶数列的联通块,显然可以构造
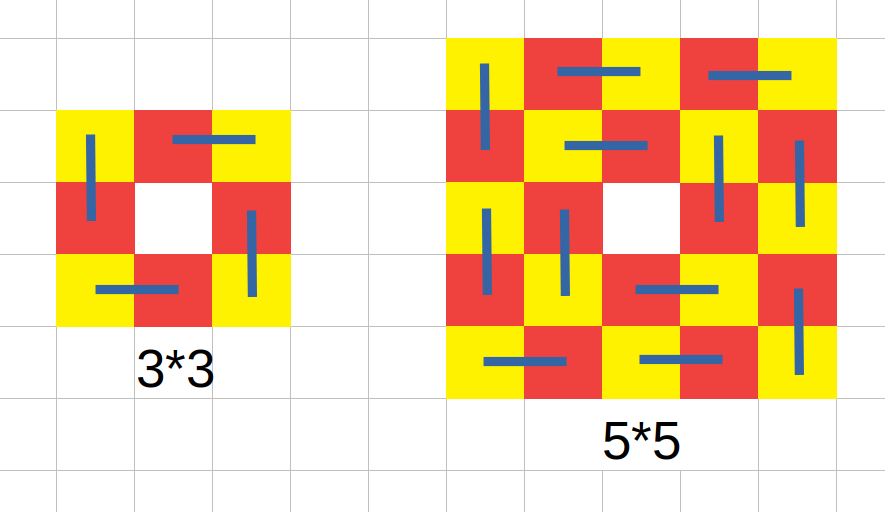
- 奇数行奇数列:这个稍微麻烦一点,我们可以选择他周围的奇数行奇数列的一个子矩阵,显然可以螺旋式的构造,也就是说我们用完左上角,对于剩下的容易证明也是两个偶数的联通块,同样可以构造,看图
3.显然是不能获得自由的,因为我们可以将这个棋盘黑白二染色,然后可以发现对顶角颜色相同,每一步颜色都会反转,一共要走63步,所以最后一步一定会在异色块上,所以不行.
4.(a)对于每一个$n$来说我们直接考虑最后一块的摆放方法,如果是竖着放,那么剩下的就是$f(n-1)$的子问题,如果是横着放,那么倒数第二块显然也是横着放的,所以剩下的就是$f(n-2)$的子问题,所以显然可以得到的是$f(n) = f(n-1)+f(n-2)$,也就是说答案就是fibonacci.$\therefore f(12) = 233$
4.(b)这里我们可以考虑DP来做,具体程序如下:
1 |
|
然后可以发现$g(n) = 4\ast g(n-2)-g(n-4)$
5.用4.(b)的代码容易可得,$g(4) = 11$
6.同样采用反证法容易证得$n$是偶数,下面我们考虑$n$是奇数扣掉中间一块的情况.不妨假设八个角上的颜色是黑色,可以得到黑块数量是$4k^3+6k^2+3k+1$,白块的数量是$4k^3+6k^2+3k$,我们可以分两种情况讨论,我们假设$n = 2k+1$
- 当k是奇数时,也就是$k = 2t+1$,即$n = 4t+3$,中间块是白色的.然后扣掉白块后,显然黑块和白块不匹配,然后不行鸭.
- 当k是偶数时,也就是$k = 2t$,即$n = 4t+1$,中间块是黑色的,扣掉黑块后,白块和黑块是匹配的,可能可以.下面我们证明$n = 4t+1$时是可行的
- 我们按照层数拆分,我们抽掉其中的第$2t+1$层,我们可以得到,这一层显然是可行的,类比于二阶的时候,我们扣掉中心块
- 对于剩下的两个联通块,我们显然可以得到是他们对称,我们只考虑上面的$2t$层的部分,我们每两层考虑一下
- 对于相连的两层,也就是$2\ast n\ast n$的形状,我们显然可以构造,所以整个三维结构是可以构造的.
7.首先证明$a$既是$n$的因子,又是$m$的因子
- 因为$a$是$b$的因子,所以$a\ast b$的可以看成多个$a\ast a$的,采用反证法,假设$a$不是$m$的因子,那么对于剩下的$(m%a)\ast (n%a)$的矩阵显然不可以用$a\ast a$的矩阵填满,所以$m%a==0&&n%a==0$.
再证$b$是$n$或者$m$的因子
- 同样反证法,我们将$a,b,m,n$同时缩小$a$倍,然后可以转化成,现在有一个$x\ast y$的棋盘,我要用一个$1\ast z$的棋盘去覆盖他,但是$gcd(x,z)=gcd(y,z)=1$,这个可以显然发现是不可能的
8.先证:存在完美覆盖$\rightarrow$存在平凡完美覆盖
- 利用习题7,我们得到如果存在完美覆盖,那么$gcd(n,a)=gcd(m,a)=a$并且$gcd(m,b)=b$,然后我们显然可以让$b$的朝向指向$m$的方向,也就是存在平凡完美覆盖
再证:存在平凡完美覆盖$\rightarrow$存在完美覆盖
- 显然
9.显然,举个简单例子$n=5,m=6,a=2,b=3$存在完美覆盖,但是不存在平凡完美覆盖.
10.假设存在不妨设四个变量是$a,b,c,d$,那么可以得到$a+b=b+c$即$a=c$显然不能构成幻方
11.12.13 如图
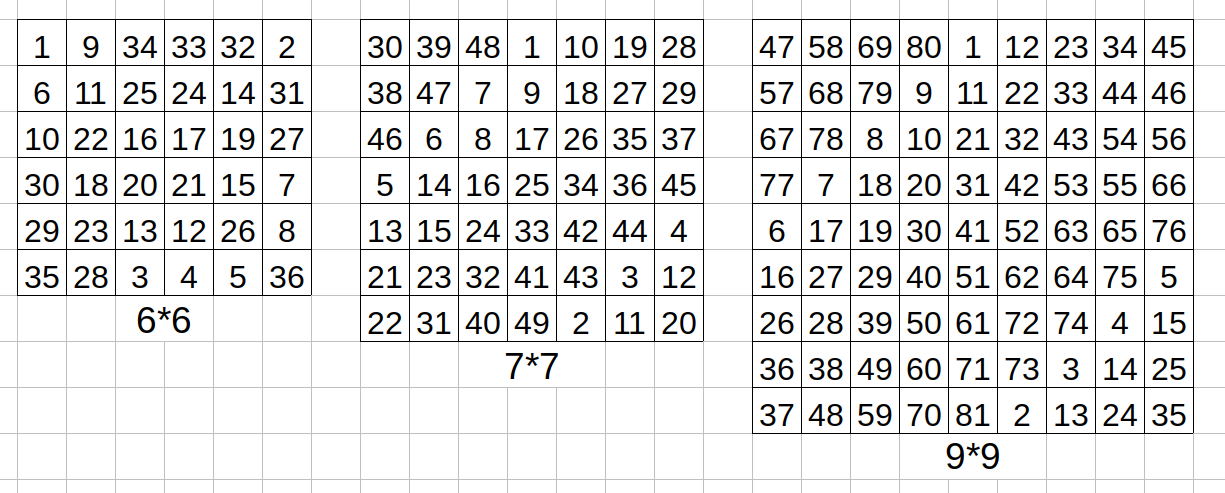
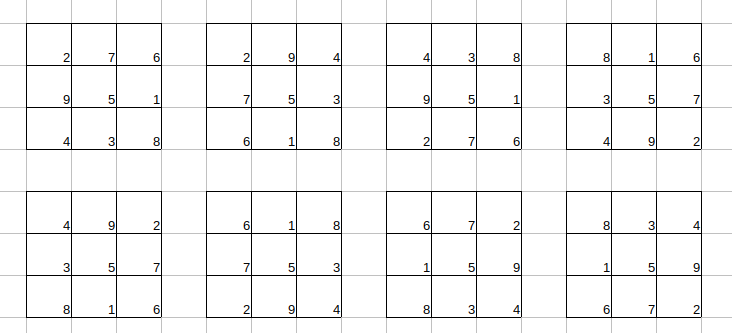
14.所有可能的构造如图
15.暴力枚举的,确实没有解,并不知道为什么……
16.$n$阶幻方,幻方总和是$n^2\ast (n^2+1)/2$,所以每一行每一列求和都是$n\ast (n^2+1)/2$,现在替换后每一行每一列的和换成了$n\ast (n^2+1) - n\ast (n^2+1)/2 = n\ast (n^2+1)/2$所以可能是个幻方,然后因为里面的元素都是属于$[1,n^2]$之间的,所以$n^2+1-a$可以保证换完之后每个元素还是只出现一次,所以新生成的还是幻方.
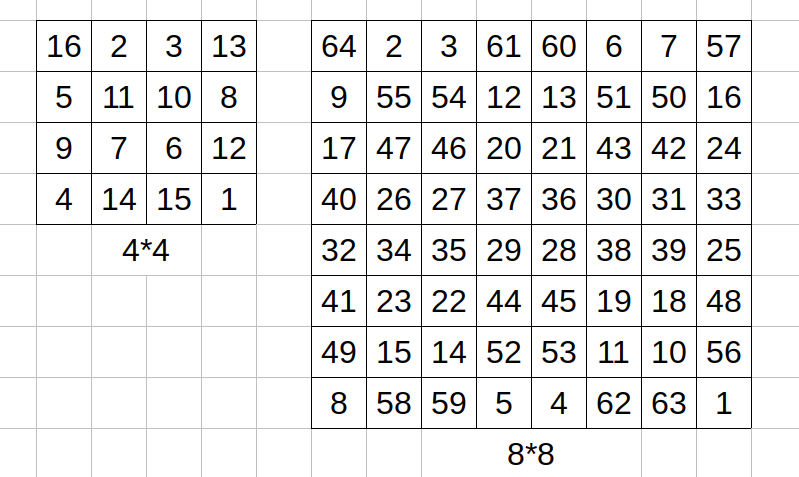
17.给出$n=4$和$n=8$时的图…….
18.这个应该是显然的,因为二阶幻方都没有,显然没有二阶幻方体.
19.首先我们拆开来看没一个单独的平面,我们可以得到,对于一个四阶幻方来说,如果对角线也满足幻和,那么显然可以得到任意三阶子矩阵的对顶角之和等于幻和的一半,所以我们任取出四阶幻方体的任一三阶子体,可以得到类似于$a+b=b+c$的等式,也就是说存在$a==c$的情况,这显然和题意不符,所以不可能存在四阶幻方体.
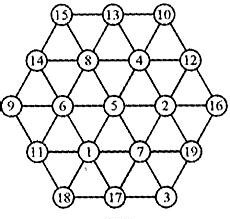
20.首先,$10$和$5$一个颜色,$1,3,7,9$一个颜色,$2,4,6,8$一种颜色,可以得到可以由三种颜色构成,然后,$1,2,10$相互接壤,显然需要三种及以上颜色来涂,方案数为$3\ast 2\ast 1 = 6$.
21.(a) 二阶的显然不存在,书后面给了答案,还有一个比较简单的想法就是如果存在显然可以得到类似于$a==b$的结论,所以不存在.
(b) 暴搜剪枝,emmmmm……如图