A. Serval and Bus
题目描述
It is raining heavily. But this is the first day for Serval, who just became 3 years old, to go to the kindergarten. Unfortunately, he lives far from kindergarten, and his father is too busy to drive him there. The only choice for this poor little boy is to wait for a bus on this rainy day. Under such circumstances, the poor boy will use the first bus he sees no matter where it goes. If several buses come at the same time, he will choose one randomly.
Serval will go to the bus station at time $t$, and there are $n$ bus routes which stop at this station. For the $i$-th bus route, the first bus arrives at time $s_i$ minutes, and each bus of this route comes $d_i$ minutes later than the previous one.
As Serval’s best friend, you wonder which bus route will he get on. If several buses arrive at the same time, you can print any of them.
Input
The first line contains two space-separated integers $n$ and $t$ (1≤$n$≤100, 1≤$t$≤$10^5$) $-$ the number of bus routes and the time Serval goes to the station.
Each of the next $n$ lines contains two space-separated integers $s_i$ and $d_i$ (1≤$s_i,d_i$≤$10^5$) $-$ the time when the first bus of this route arrives and the interval between two buses of this route.
Output
Print one number $-$ what bus route Serval will use. If there are several possible answers, you can print any of them.
Examples
input1
2 2
6 4
9 5
output1
1
input2
5 5
3 3
2 5
5 6
4 9
6 1
output2
3
input3
3 7
2 2
2 3
2 4
output3
1
题意
zuhiul很忙,他要约妹子,他一共有$n$个妹子要约,但是他$t$天后才有空,妹子们也不是每天都有时间,但是妹子都是周期性有时间,比如,第$i$个妹子,$s_i$天之后才有时间,而且每$d_i$天就会再次出线,现在问你,zuhiul最早会和哪个妹子约会,如果会和多个妹子约会,只需要输出任意一个妹子就行了。
分析
只需要枚举每个妹子,然后看一下这个妹子什么时候最早可以邀约,然后算一下min就可以了
代码
给大佬递上我奇丑无比的代码 (/ω\)
1 |
|
B. Serval and Toy Bricks
题目描述
Luckily, Serval got onto the right bus, and he came to the kindergarten on time. After coming to kindergarten, he found the toy bricks very funny.
He has a special interest to create difficult problems for others to solve. This time, with many $1\times 1\times 1$ toy bricks, he builds up a 3-dimensional object. We can describe this object with a $n\times m$ matrix, such that in each cell $(i,j)$ , there are $h_{i,j}$ bricks standing on the top of each other.
However, Serval doesn’t give you any $h_{i,j}$, and just give you the front view, left view, and the top view of this object, and he is now asking you to restore the object. Note that in the front view, there are $m$ columns, and in the $i$-th of them, the height is the maximum of $h_{1,i},h_{2,i},\dots,h_{n,i}$. It is similar for the left view, where there are $n$ columns. And in the top view, there is an 𝑛×𝑚 matrix $t_{i,j}$, where $t_{i,j}$ is 0 or 1. If $t_{i,j}$ equals 1, that means $h_{i,j}$>0, otherwise, $h_{i,j}$=0.
However, Serval is very lonely because others are bored about his unsolvable problems before, and refused to solve this one, although this time he promises there will be at least one object satisfying all the views. As his best friend, can you have a try?
Input
The first line contains two space-separated integers $n$ and $t$ (1≤$n$≤100, 1≤$t$≤$10^5$) $-$ the number of bus routes and the time Serval goes to the station.
Each of the next $n$ lines contains two space-separated integers $s_i$ and $d_i$ (1≤$s_i,d_i$≤$10^5$) $-$ the time when the first bus of this route arrives and the interval between two buses of this route.
Output
Print one number $-$ what bus route Serval will use. If there are several possible answers, you can print any of them.
Examples
input1
3 7 3
2 3 0 0 2 0 1
2 1 3
1 0 0 0 1 0 0
0 0 0 0 0 0 1
1 1 0 0 0 0 0
output1
1 0 0 0 2 0 0
0 0 0 0 0 0 1
2 3 0 0 0 0 0
input2
4 5 5
3 5 2 0 4
4 2 5 4
0 0 0 0 1
1 0 1 0 0
0 1 0 0 0
1 1 1 0 0
output2
0 0 0 0 4
1 0 2 0 0
0 5 0 0 0
3 4 1 0 0
Note
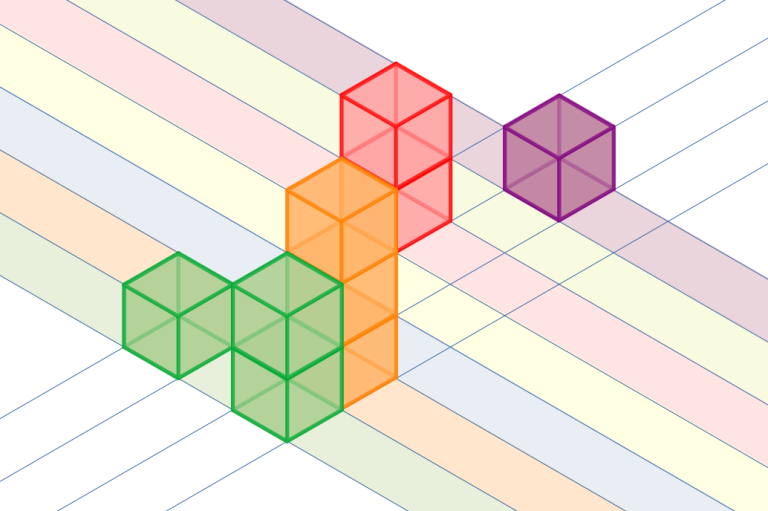
The graph above illustrates the object in the first example.
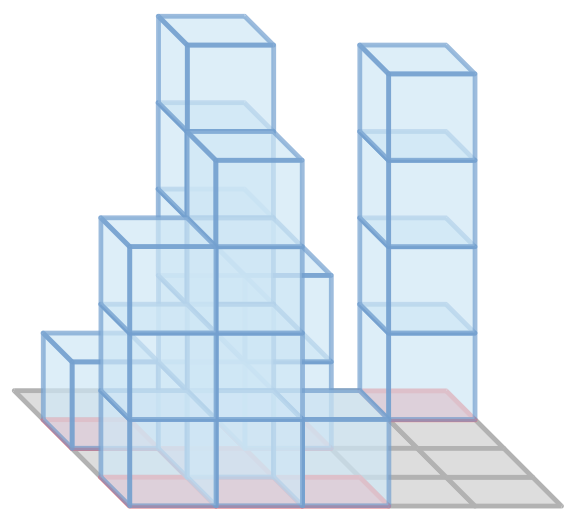
The first graph illustrates the object in the example output for the second example, and the second graph shows the three-view drawing of it.
题意
zuhiul和妹子玩游戏,妹子搭了一个积木,然后zuhiul猜积木长啥样,zuhiul必然不会,于是小姐姐放过了他,告诉了他现在的主视图,侧视图和俯视图,然后让zuhiul猜,zuhiul还是不会,但是为了脸面不能说不会,然后来问你了。你需要输出一种可能的解满足这个三视图。
分析
告诉了主视图和左视图,相当于限制了最大值,告诉俯视图相当于告诉哪里可能有方块。然后枚举俯视图的每个位置,输出答案即可。
代码
给大佬递上我奇丑无比的代码 (/ω\)
1 |
|
C. Serval and Parenthesis Sequence
题目描述
Serval soon said goodbye to Japari kindergarten, and began his life in Japari Primary School.
In his favorite math class, the teacher taught him the following interesting definitions.
A parenthesis sequence is a string, containing only characters “(“ and “)”.
A correct parenthesis sequence is a parenthesis sequence that can be transformed into a correct arithmetic expression by inserting characters “1” and “+” between the original characters of the sequence. For example, parenthesis sequences “()()”, “(())” are correct (the resulting expressions are: “(1+1)+(1+1)”, “((1+1)+1)”), while “)(“ and “)” are not. Note that the empty string is a correct parenthesis sequence by definition.
We define that $|s|$ as the length of string $s$. A strict prefix $s[1\dots l]$ (1 ≤ $l$ < $|s|$) of a string $s=s_{1}s_{2}\dots s_{|s|}$ is string $s_{1}s_{2}\dots s_{l}$. Note that the empty string and the whole string are not strict prefixes of any string by the definition.
Having learned these definitions, he comes up with a new problem. He writes down a string $s$ containing only characters “(“, “)” and “?”. And what he is going to do, is to replace each of the “?” in $s$ independently by one of “(“ and “)” to make all strict prefixes of the new sequence not a correct parenthesis sequence, while the new sequence should be a correct parenthesis sequence.
After all, he is just a primary school student so this problem is too hard for him to solve. As his best friend, can you help him to replace the question marks? If there are many solutions, any of them is acceptable.
Input
The first line contains a single integer $|s|$ (1≤$|s|$≤$3\cdot 10^5$), the length of the string.
The second line contains a string $s$, containing only “(“, “)” and “?”.
Output
A single line contains a string representing the answer.
If there are many solutions, any of them is acceptable.
If there is no answer, print a single line containing “:(“ (without the quotes).
Examples
input1
6
(?????
output1
(()())
input2
10
(???(???(?
output2
:(
Note
It can be proved that there is no solution for the second sample, so print “:(“.
题意
给你一堆左括号右括号和问号,问你能否把问号变成左括号或者右括号,使得这个变成一个括号匹配的序列,并且序列的任何前缀不是一个括号匹配序列。
分析
显然对于后一个条件,我们只需要让最左边的左括号和最右边的右括号匹配就行了,然后中间是一个括号匹配序列就行了。然后填充的时候贪心的让左边填充左括号,右边填充右括号,然后check一下就行了.
代码
给大佬递上我奇丑无比的代码 (/ω\)
1 |
|
D. Serval and Rooted Tree
题目描述
Now Serval is a junior high school student in Japari Middle School, and he is still thrilled on math as before.
As a talented boy in mathematics, he likes to play with numbers. This time, he wants to play with numbers on a rooted tree.
A tree is a connected graph without cycles. A rooted tree has a special vertex called the root. A parent of a node $v$ is the last different from $v$ vertex on the path from the root to the vertex $v$. Children of vertex $v$ are all nodes for which $v$ is the parent. A vertex is a leaf if it has no children.
The rooted tree Serval owns has $n$ nodes, node 1 is the root. Serval will write some numbers into all nodes of the tree. However, there are some restrictions. Each of the nodes except leaves has an operation max or min written in it, indicating that the number in this node should be equal to the maximum or minimum of all the numbers in its sons, respectively.
Assume that there are $k$ leaves in the tree. Serval wants to put integers $1,2,\dots,k$ to the $k$ leaves (each number should be used exactly once). He loves large numbers, so he wants to maximize the number in the root. As his best friend, can you help him?
Input
The first line contains an integer $n$ (2≤$n$≤$3\cdot 10^5$), the size of the tree.
The second line contains $n$ integers, the $i$-th of them represents the operation in the node $i$. 0 represents min and 1 represents max. If the node is a leaf, there is still a number of 0 or 1, but you can ignore it.
The third line contains $n-1$ integers $f_2,f_3,\dots,f_n$ (1≤$f_i≤$i-1$), where $f_i$ represents the parent of the node $i$.
Output
Output one integer $-$ the maximum possible number in the root of the tree.
Examples
input1
6
1 0 1 1 0 1
1 2 2 2 2
output1
1
input2
5
1 0 1 0 1
1 1 1 1
output2
4
input3
8
1 0 0 1 0 1 1 0
1 1 2 2 3 3 3
output3
4
input4
9
1 1 0 0 1 0 1 0 1
1 1 2 2 3 3 4 4
output4
5
Note
Pictures below explain the examples. The numbers written in the middle of the nodes are their indices, and the numbers written on the top are the numbers written in the nodes.
In the first example, no matter how you arrange the numbers, the answer is $1$.
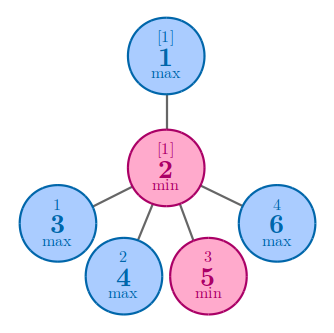
In the second example, no matter how you arrange the numbers, the answer is $4$.
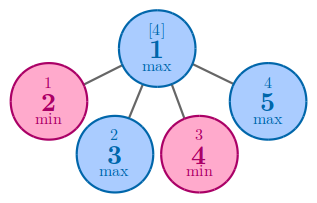
In the third example, one of the best solution to achieve $4$ is to arrange $4$ and $5$ to nodes $4$ and $5$.
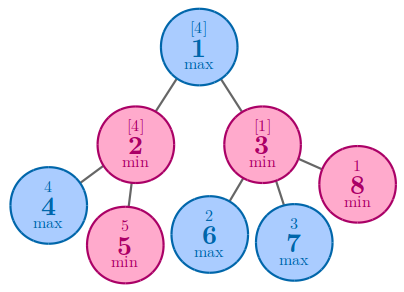
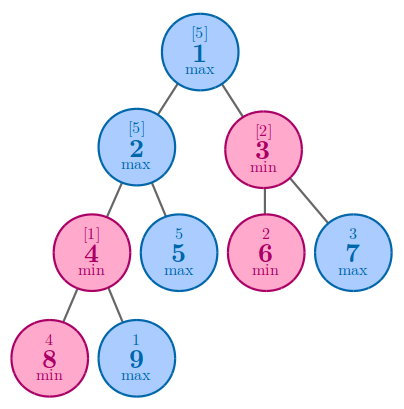
In the fourth example, the best solution is to arrange $5$ to node $5$.
题意
给你一颗有根树,每个非叶节点上有一个函数,可能为min或者max,你需要在k个叶节点上填上$1,2,\dots,k$,使得经过非叶节点的操作之后,根节点的值最大。
分析
显然是要分析函数的作用。
如果是取max,说明所有的子节点中,我们可以把某一个子节点的值取到最大,然后其他的节点全塞垃圾值。
如果是取min,说明所有子节点都起作用,说明我们对于每个子节点都要尽可能的大。
然后就可以得到,max的策略是,找到孙子节点最少的子节点,填充大值,min的策略是,对所有子节点求和。
然后这样得到的就是所有对答案有贡献的节点数,然后用总结点数减去贡献节点数就是答案。
代码
给大佬递上我奇丑无比的代码 (/ω\)
1 |
|
E. Serval and Snake
题目描述
This is an interactive problem.
Now Serval is a senior high school student in Japari Middle School. However, on the way to the school, he must go across a pond, in which there is a dangerous snake. The pond can be represented as a $n\times n$ grid. The snake has a head and a tail in different cells, and its body is a series of adjacent cells connecting the head and the tail without self-intersecting. If Serval hits its head or tail, the snake will bite him and he will die.
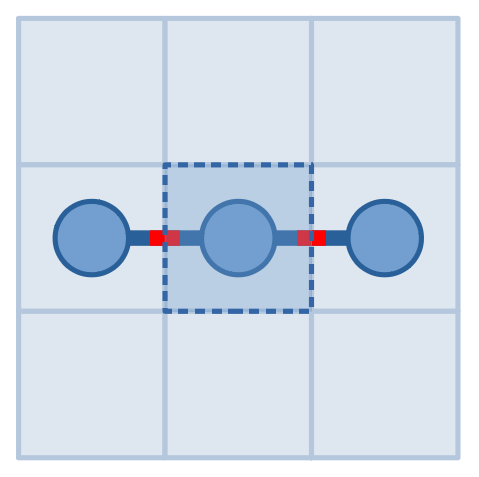
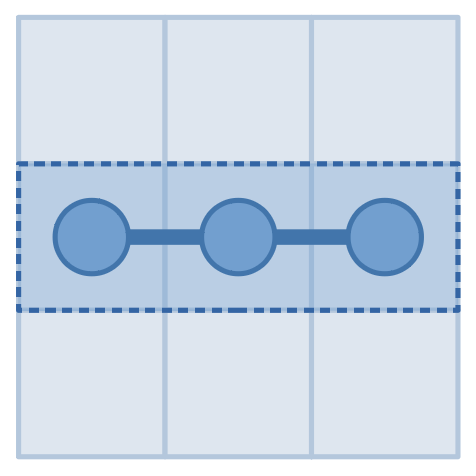
Luckily, he has a special device which can answer the following question: you can pick a rectangle, it will tell you the number of times one needs to cross the border of the rectangle walking cell by cell along the snake from the head to the tail. The pictures below show a possible snake and a possible query to it, which will get an answer of $4$.
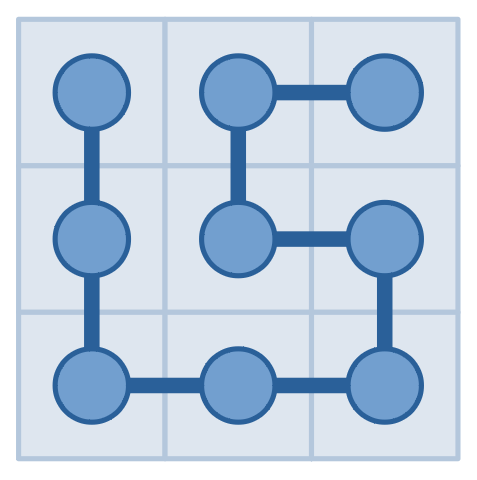
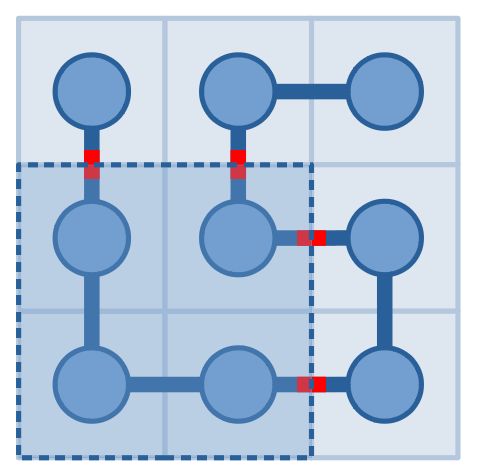
Today Serval got up too late and only have time to make 2019 queries. As his best friend, can you help him find the positions of the head and the tail?
Note that two cells are adjacent if and only if they have a common edge in the grid, and a snake can have a body of length 0, that means it only has adjacent head and tail.
Also note that the snake is sleeping, so it won’t move while Serval using his device. And what’s obvious is that the snake position does not depend on your queries.
Input
The first line contains a single integer $n$ (2≤$n$≤1000) $-$ the size of the grid.
Output
When you are ready to answer, you should print ! x1 y1 x2 y2, where $(x_1,y_1)$ represents the position of the head and $(x_2,y_2)$ represents the position of the tail. You can print head and tail in any order.
Interaction
To make a query, you should print ? x1 y1 x2 y2 (1≤$x_1$≤$x_2$≤𝑛, 1≤$y_1$≤$y_2$≤$n$), representing a rectangle consisting of all cells $(x,y)$ such that $x_1$≤$x$≤$x_2$ and $y_1$≤$y$≤$y_2$. You will get a single integer as the answer.
After printing a query, do not forget to output the end of line and flush the output, otherwise you will get Idleness limit exceeded. To do this, use:
- fflush(stdout) or cout.flush() in C++;
- System.out.flush() in Java;
- flush(output) in Pascal;
- stdout.flush() in Python;
see documentation for other languages.
Answer $-1$ instead of a valid answer means that you made an invalid query or exceeded the maximum number of queries. Exit immediately after receiving $-1$ and you will see Wrong answer verdict. Otherwise you can get an arbitrary verdict because your solution will continue to read from a closed stream.
If your program cannot find out the head and tail of the snake correctly, you will also get a Wrong Answer verdict.
Hacks
To make a hack, print a single integer $n$ (2≤$n$≤1000) in the first line, indicating the size of the grid.
Then print an integer $k$ (2≤$k$≤𝑛2) in the second line, indicating the length of the snake.
In the next $k$ lines, print $k$ pairs of integers $x_i,y_i$ (1≤$x_i,y_i$≤𝑛), each pair in a single line, indicating the $i$-th cell of snake, such that the adjacent pairs are adjacent, and all $k$ pairs are distinct.
Examples
input1
2
1
0
0
output1
? 1 1 1 1
? 1 2 1 2
? 2 2 2 2
! 1 1 2 1
input2
3
2
0
output2
? 2 2 2 2
? 2 1 2 3
! 2 1 2 3
Note
The pictures above show our queries and the answers in the first example. We first made a query for (1,1) and got an answer 1, then found that it must be connected to exactly one other cell. Then we made a query for (1,2) and got an answer of 0, then knew that the snake never entered it. So the cell connected to (1,1) must be (2,1). Then we made a query for (2,2) and got an answer 0, then knew that it never entered (2,2) as well. So the snake cannot leave (2,1), which implies that the answer is (1,1) and (2,1).
The pictures above show our queries and the answers in the second example. By making query to (2,2) and receiving 2, we found that the snake occupies (2,2). And by making query to rectangle from (2,1) to (2,3) and receiving answer 0, we knew that it never goes out of the rectangle from (2,1) to (2,3). Since the first answer is 2, both (2,1) and (2,3) must be occupied but none of others, so the answer is (2,1) and (2,3).
题意
现在有一条蛇在一个方格图中,你可以给出不超过2019次询问,每次询问一个矩形,回答是,你用这个矩形去切蛇,可以得到这个蛇被切了多少刀,现在问你蛇头和蛇尾的位置。
分析
首先我们可以观察到,当一个矩形切下去之后发现切了奇数刀,那么可以有必然存在一个头或者尾在矩形中。
然后我们可以用$(n-1)<<1$次询问得到所有的行和列对应的切的次数。
然后可以证明的是,所有的数据中必然存在奇数。反证法易得。
然后可以证明奇数对应的行或者列左右必然存在头或者尾。
所以可以得到一个很直观的$O(6n)$的做法,$2n$用来寻找,剩下的$4n$来搜索答案。但是这必然会超过2019.
考虑哪些步骤可以优化?
$2n$不可优化,必然就只能优化搜索过程。
需要注意的是,可能存在行或者列不存在奇数的情况,稍微分析可以得到这种情况的特点了,头和尾在同一行或者同一列中。
我们考虑到,我们只用考虑奇偶的情况,而不用考虑具体值。
因为奇偶的加减特性,我们可以二分这个答案。
除此之外,如果行和列都有奇数值,那么可以得到行和列对应的四个点中,两个点是答案,枚举任何一个就可以得到答案。
代码
给大佬递上我奇丑无比的代码 (/ω\)
1 |
|
F. Serval and Bonus Problem
题目描述
Getting closer and closer to a mathematician, Serval becomes a university student on math major in Japari University. On the Calculus class, his teacher taught him how to calculate the expected length of a random subsegment of a given segment. Then he left a bonus problem as homework, with the award of a garage kit from IOI. The bonus is to extend this problem to the general case as follows.
You are given a segment with length $l$. We randomly choose $n$ segments by choosing two points (maybe with non-integer coordinates) from the given segment equiprobably and the interval between the two points forms a segment. You are given the number of random segments $n$, and another integer $k$. The $2n$ endpoints of the chosen segments split the segment into ($2n+1$) intervals. Your task is to calculate the expected total length of those intervals that are covered by at least $k$ segments of the $n$ random segments.
You should find the answer modulo $998244353$.
Input
First line contains three space-separated positive integers 𝑛, 𝑘 and 𝑙 ($1\leq k\leq n\leq 2000,1\leq l\leq 10^9$).
Output
Output one integer — the expected total length of all the intervals covered by at least $k$ segments of the $n$ random segments modulo $998244353$.
Formally, let $M=998244353$. It can be shown that the answer can be expressed as an irreducible fraction $\frac{p}{q}$, where $p$ and $q$ are integers and $q\not\equiv0(modM)$. Output the integer equal to $p\cdot q^{-1}mod\ M$. In other words, output such an integer $x$ that $0\leq x<M$ and $x\cdot q\equiv p(mod\ M)$.
Examples
inpus1
1 1 1
output1
332748118
input2
6 2 1
output2
760234711
input3
7 5 3
output3
223383352
input4
97 31 9984524
output4
267137618
Note
In the first example, the expected total length is $\int_0^1 \int_0^1 |x-y|\ dx\ dy = \frac{1}{3} $, and $\frac{1}{3}$ modulo $998244353$ is $332748118$.
题意
长度为l的线段,随机选取n个线段,线段中至少被n个线段中k个线段覆盖的长度期望。
分析
说实话我当时没做出来,看了题解才知道怎么做的,所以强烈建议看官方的题解。我这里也贴出来,感兴趣的可以看一下。
Without loss of generality, assume that $l$=1. For a segment covering, the total length of the legal intervals is the probability that we choose another point $P$ on this segment randomly such that it is in the legal intervals. Since all $2n+1$ points ($P$ and the endpoints of each segment) are chosen randomly and independently, we only need to find the probability that point $P$ is in the legal intervals. Note that only the order of these $2n+1$ points make sense. Because the points are chosen in the segment, the probability that some of them coincide is $0$, so we can assume that all points do not coincide.
Now the problem is, how to calculate the number of arrangements that $P$ is between at least $k$ pairs of endpoints. It can be solved by dynamic programming in time complexity of $O(n^2)$. We define $f(i,j,x)$ as the number of arrangements for the first $i$ positions, with $j$ points haven’t been matched, and $P$ appeared $x$ times (obviously $x=0$ or $1$). So we can get three different types of transition for the $i$-th position below:
- Place $P$ at $i$-th position (if $j\geq k$): $f(i-1,j,0)\rightarrow f(i,j,1)$
- Start a new segment (if $i+j+x<2n$): $f(i-1,j-1,x)\rightarrow f(i,j,x)$
- Match a started segment, note that we have 𝑗 choices of segments:$f(i-1,j+1,x)\times(j+1)\rightarrow f(i,j,x)$
Then $f(2n+1,0,1)$ is the number of legal arrangements. Obviously, the total number of arrangements is $(2n+1)!$. However, there are 𝑛 pairs of endpoints whose indices can be swapped, and the indices 𝑛 segments can be rearranged. So the final answer is $\frac{f(2n+1,0,1)\times n!\times 2^n}{(2n+1)!}$.
可能是受了题解的影响,后来也没想出来其他解法。
这里讲一下题解怎么做的。
首先我们可以发现,长度和答案成正比,也就是说如果长度为1的时候答案是a,那么长度为2的时候答案就是2a%mod.
然后我们不妨设长度为1,最后答案乘上l就行了。
然后因为我们要找到至少被线段覆盖k次的所有点,所以我们不如加上一个虚拟点,这样就一共有了$(n<<1|1)$个点,然后需要判断这个虚拟点被多少条线段覆盖了,如果覆盖次数超过k次,就说明可以统计进答案。然后就可以发现,所有点是随机取的,所以我们假设所有点不会重合,那么所有点就可以离散成一个序列。然后就可以统计k的覆盖次数。
接下来就是dp,我们设$dp[i][j][flag]$表示序列中前i个点,其中到目前为止有j条线段左节点出线了,但是右节点没有出现,也就是说当前这个点被覆盖了j次,flag表示虚拟点是否出现了。然后考虑转移:
- 当前节点是虚拟节点
- 如果这个需要统计进入答案,也就是说明当前节点需要被覆盖k次及以上,所以 $j\geq k$
- $dp[i][j][1]+=dp[i-1][j][0]$
- 当前节点是一个线段的左端点
- 也就是说左节点数量增加,被覆盖次数增加,但是不会影响虚拟节点的状态
- $dp[i][j+1][flag]+=dp[i-1][j][flag]$
- 当前节点是一个线段的右端点
- 也就是说右节点数量增加,被覆盖次数减少,但是不会影响虚拟节点的状态,注意右端点可能会有j个可能
- $dp[i][j-1][flag]+=dp[i-1][j][flag]*j$
代码
给大佬递上我奇丑无比的代码 (/ω\)
1 |
|

