Codeforces 761 E

E. Dasha and Puzzle

开启传送门

题目描述

Dasha decided to have a rest after solving the problem. She had been ready to start her favourite activity — origami, but remembered the puzzle that she could not solve.

The tree is a non-oriented connected graph without cycles. In particular, there always are $n - 1$ edges in a tree with $n$ vertices.

The puzzle is to position the vertices at the points of the Cartesian plane with integral coordinates, so that the segments between the vertices connected by edges are parallel to the coordinate axes. Also, the intersection of segments is allowed only at their ends. Distinct vertices should be placed at different points.

Help Dasha to find any suitable way to position the tree vertices on the plane.

It is guaranteed that if it is possible to position the tree vertices on the plane without violating the condition which is given above, then you can do it by using points with integral coordinates which don’t exceed $10^{18}$ in absolute value.

Input

The first line contains single integer $n$ ($1 ≤ n ≤ 30$) — the number of vertices in the tree.

Each of next $n - 1$ lines contains two integers $u_i, v_i$ ($1 ≤ u_i, v_i ≤ n$) that mean that the $i$-th edge of the tree connects vertices $u_i$ and $v_i$.

It is guaranteed that the described graph is a tree.

Output

If the puzzle doesn’t have a solution then in the only line print “NO”.

Otherwise, the first line should contain “YES”. The next n lines should contain the pair of integers $x_i$, $y_i$ (|$x_i$|, |$y_i$| ≤ $10^{18}$) — the coordinates of the point which corresponds to the $i$-th vertex of the tree.

If there are several solutions, print any of them.

Examples

input1

7

1 2

1 3

2 4

2 5

3 6

3 7

output1

YES

0 0

1 0

0 1

2 0

1 -1

-1 1

0 2

input2

6

1 2

2 3

2 4

2 5

2 6

output2

NO

input3

4

1 2

2 3

3 4

output3

YES

3 3

4 3

5 3

6 3

Note

In the first sample one of the possible positions of tree is:

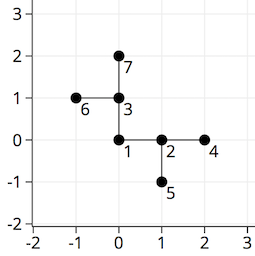
题意

zuhiul认识很多妹子（不超过30个），妹子之间是个树形关系。zuhiul家很大，所以他想把所有妹子放家里，因为zuhiul比较喜欢整点，所以他希望妹子都在整点上，并且有关系的妹子，他们之间的连线平行于坐标轴，并且关系不能相交，也不能重合（贵圈真乱！）。虽然zuhiul很有钱，但是他家也不是无限大，也即：所有妹子的坐标的绝对值不能超过$10^{18}$。

分析

显然的构造题。

首先因为妹子的关系不能相交，并且要平行于坐标轴，所以可以得到如果一个妹子和四个以上的妹子有关系，那么显然就不能构造出来。首先处理这种非法情况。

剩下的显然是一个dfs搞一下，因为无根，直接取$1$为根。

然后显然是找一个比较好的展开方式就行了。一个直观的做法就是按层次展开就行了。但是为了保证关系不交。我们考虑用下面两个规则展开。

• 1.每层的距离至多为前一层的$\frac{1}{2}$。
• 2.同层的节点的距离不同。

这样可以保证所有的点在四相扩展的时候不交。

代码

给大佬递上我奇丑无比的代码　(/ω＼)

#include<bits/stdc++.h>
using namespace std;
int n;
vector<int> son[100];
long long dirx[] = {1,-1,0,0};
long long diry[] = {0,0,1,-1};
bool has_position[100];
long long ansx[100],ansy[100];
void lay(int ind, int pre, long long x,long long y, int dir, int floor) {
	has_position[ind] = true;
	ansx[ind] = x;
	ansy[ind] = y;
	long long rdis = 1ll<<floor;
	int dir_ind = 0;
	for(int i:son[ind]) {
		if(i==pre) continue;
		if(dir_ind==(dir^1)) dir_ind++;
		if(dir_ind>3) {
			printf("NO");
			exit(0);
		}
		lay(i, ind, x+dirx[dir_ind]*rdis, y+diry[dir_ind]*rdis, dir_ind, floor-1);
		rdis--;
		dir_ind ++ ;
	}
}
int main(){
	scanf("%d",&n);
	for(int i = 1, from ,to;i<n;i++) {
		scanf("%d%d",&from,&to);
		son[from].push_back(to);
		son[to].push_back(from);
	}
	lay(1,0,0,0,-1,50);
	for(int i = 1;i<=n;i++) if(!has_position[i]) {
		printf("NO\n");
		return 0;
	}
	printf("YES\n");
	for(int i = 1;i<=n;i++) printf("%lld %lld\n", ansx[i], ansy[i]);
	return 0;
}