Codeforces 1187 E

E. Tree Painting

题目描述

You are given a tree (an undirected connected acyclic graph) consisting of $n$ vertices. You are playing a game on this tree.

Initially all vertices are white. On the first turn of the game you choose one vertex and paint it black. Then on each turn you choose a white vertex adjacent (connected by an edge) to any black vertex and paint it black.

Each time when you choose a vertex (even during the first turn), you gain the number of points equal to the size of the connected component consisting only of white vertices that contains the chosen vertex. The game ends when all vertices are painted black.

Let’s see the following example:

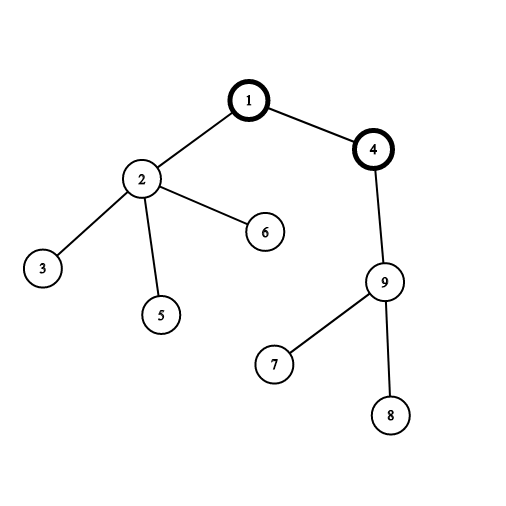
Vertices $1$ and $4$ are painted black already. If you choose the vertex $2$, you will gain $4$ points for the connected component consisting of vertices $2,3,5$ and $6$. If you choose the vertex $9$, you will gain $3$ points for the connected component consisting of vertices $7,8$ and $9$.

Your task is to maximize the number of points you gain.

Input

The first line contains an integer $n$ — the number of vertices in the tree ($2≤n≤2⋅10^5$).

Each of the next $n−1$ lines describes an edge of the tree. Edge $i$ is denoted by two integers $u_i$ and $v_i$, the indices of vertices it connects ($1≤u_i,v_i≤n$, $u_i\neq v_i$).

It is guaranteed that the given edges form a tree.

Output

Print one integer — the maximum number of points you gain if you will play optimally.

Examples

input1

1 2

2 3

2 5

2 6

1 4

4 9

9 7

9 8

output1

input2

1 2

1 3

2 4

2 5

output2

Note

The first example tree is shown in the problem statement.

题意

zuhiul认识很多妹子（不超过$2\cdot 10^5$个），妹子之间是个树形关系。他决定每天聊一个妹子，但是他是个强迫症，第一天他可以随便聊任何一个妹子，但是之后每一天，他只能聊和之前聊过的妹子有关系的妹子。每次聊一个妹子之前，他会数一下这个妹子所在的未聊过的连通块的大小，当然，连通块越大他越开心（连通块为 $n$ ，他会得到 $n$ 开心度），现在问你，他聊完所有妹子后，开心度求和后为多少。

分析

如果我们强制第一次聊编号为 $1$ 的妹子，我们考虑怎么统计答案。

一个很直观的想法是，我们可以一次dfs出所有子树的大小，然后对于每棵子树大小求和就是答案。

那么现在问题就转化成了，如何对于每个根求答案。

显然换根可解，但是如何统计换根后的答案呢？

我们考虑一下，我们以 $1$ 为根的时候怎么算的答案呢？

每棵子树的大小求和。但是我们可以换个角度看问题，我们不看子树的贡献，我们考虑每个节点的贡献，可以显然的发现，每个节点的贡献就是每个节点到 $1$ 的距离。

所以换根就很直观了。我们定义 $ans[i]$ 表示以 $i$ 为根的答案，$cnt[i]$ 表示以 $1$ 为根的时候，$i$ 子树的大小。所以换根相对于当前节点的父亲的代价就是 $i$ 子树深度-1，其他节点深度+1。所以当前节点相对于父亲的答案是，减少了 $cnt[i]$，增加了 $n-cnt[i]$。也即

$$ans[ind] = ans[pre] - cnt[ind] + (n-cnt[ind]) $$

代码

给大佬递上我奇丑无比的代码　(/ω＼)

#include<bits/stdc++.h>
using namespace std;
const int maxm = 2e5+10;
int n;
vector<int> mat[maxm];
long long size[maxm];
long long ans[maxm];
void dfs(int ind = 1, int pre = 0) {
	size[ind] = 1;
	for(auto i:mat[ind]) {
		if(i==pre) continue;
		dfs(i, ind);
		size[ind] += size[i];
	}
	ans[1] += size[ind];
}
void dfs2(int ind, int pre) {
	ans[ind] = ans[pre] - size[ind] + (n-size[ind]);
	for(auto i:mat[ind]) {
		if(i==pre) continue;
		dfs2(i, ind);
	}
}
int main(){
	scanf("%d",&n);
	for(int i = 1, from, to;i<n;i++) {
		scanf("%d%d",&from,&to);
		mat[from].push_back(to);
		mat[to].push_back(from);
	}
	dfs();
	for(auto i:mat[1]) dfs2(i, 1);
	long long rans = 0;
	for(int i = 1;i<=n;i++) rans = max(rans, ans[i]);
	printf("%lld\n", rans);
	return 0;
}